프로그래머스 JS [멀쩡한 사각형]

• 멀쩡한 사각형

문제 설명

가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

제한사항

• W, H : 1억 이하의 자연수

입출력 예

WHresult

8

12

80

입출력 예 설명

입출력 예 #1
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

---

문제 풀이

 

1. 예시 이미지를 보면 특정 구간의 모양이 반복되는 것을 알 수 있습니다.

 

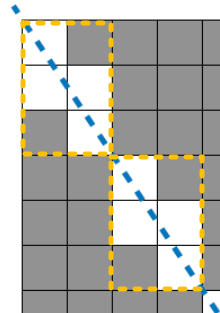
8과 12를 두 수의 최대공약수로 나눈 수인 

2*3 너비에서 반복되고 있다는 것을 가정하고

3*3, 2*4 와 같이 최대 공약수가 1이 아닌 경우를 그려보면 금방 확인할 수 있습니다.

  let 최대공약수 = 1;
  let 큰수 = Math.max(w, h);
  for (let i = 2; i <= 큰수; i++) {
    if (w % i === 0 && h % i === 0) {
      최대공약수 = i;
    }
  }

 

2. 이제 w와 h를 최대공약수로 나누어 준 서로소w와 서로소h를 이용해서
단위 당 모눈 종이의 수를 구합니다.

  let 서로소W = w / 최대공약수;
  let 서로소H = h / 최대공약수;

 

3. 2*2, 3*3, 4*4 형태의 멀쩡한 모눈의 수를 찾아보면

너비 - 멀쩡한 모눈 수

2*2 - 2

3*3 - 3

4*4 - 4

뭔가 쉬운 규칙이 보입니다.

2*3, 3*3, 4*3 한 변의 길이를 고정하고 해봅시다

2*3 - 1*2

3*3 - 2*2

4*3 - 3*2

규칙을 찾은 것 같습니다.

단위당 잘린 모눈의 수 ===>

(너비) - (서로소W-1) * (서로소H-1) ===>

(a*b) - (a-1) * (b-1) 

  let 서로소너비 = 서로소W * 서로소H;
  let 멀쩡한모눈 = (서로소W - 1) * (서로소H - 1);
  let 단위당잘린모눈수 = 서로소너비 - 멀쩡한모눈;

 

전체 너비에서 잘린 모눈의 수를 반환합니다.

  let 잘린총모눈수 = 단위당잘린모눈수 * 최대공약수;
  let 전체너비 = w * h;
  return 전체너비 - 잘린총모눈수;

 

 

 

function solution(w, h) {

  let 최대공약수 = 1;

  let 큰수 = Math.max(w, h);

  for (let i = 2; i <= 큰수; i++) {

    if (w % i === 0 && h % i === 0) {

      최대공약수 = i;

    }

  }

  let 서로소W = w / 최대공약수;

  let 서로소H = h / 최대공약수;

  let 서로소너비 = 서로소W * 서로소H;

  let 멀쩡한모눈 = (서로소W - 1) * (서로소H - 1);

  let 단위당잘린모눈수 = 서로소너비 - 멀쩡한모눈;

 

  let 잘린총모눈수 = 단위당잘린모눈수 * 최대공약수;

  let 전체너비 = w * h;

  return 전체너비 - 잘린총모눈수;

}